Potenciação de Radicais
Observando as potencias, temos que:
De modo geral, para se elevar um radical a um dado expoente, basta elevar o radicando àquele expoente. Exemplos:
Divisão de Radicais
Segundo as propriedades dos radicais, temos que:
De um modo geral, na divisão de radicais de mesmo índice, mantemos o índice e dividimos os radicais: Exemplos:
: 
= 
Se os radicais forem diferentes, devemos reduzi-los ao mesmo índice e depois efetue a operação. Exemplos:
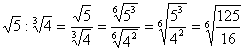
Considere a fração: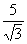 
que seu denominador é um número irracional.
que seu denominador é um número irracional.
Vamos agora multiplicar o numerador e o denominador desta fração por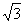 
, obtendo uma fração equivalente:
, obtendo uma fração equivalente:
Observe que a fração equivalente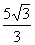 
possui um denominador racional.
possui um denominador racional.
A essa transformação, damos o nome de racionalização de denomindores.
A racionalização de denominadores consiste, portanto, na obtenção de um fração com denominador racional, equivalente a uma anterior, que possuía um ou mais radicais em seu denominador.
Para racionalizar o denominador de uma fração devemos multiplicar os termos desta fração por uma expressão com radical, denominado fator racionalizante, de modo a obter uma nova fração equivalente com denominador sem radical.
Principais casos de racionalização:
1º Caso: O denominador é um radical de índice 2: Exemplos:
é o fator racionalizante de , pois . = 
= a
2º Caso: O denominador é um radical de índice diferente de 2. Exemplos:
é o fator racionalizante de 
é o fator racionalizante de 
é o fator racionalizante de 
é o fator racionalizante de 
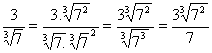
Potência com expoente racional
Observe as seguintes igualdades:
ou 
Igualmente podemos transformar uma potência com expoente fracionário em um radical.
De modo geral, definimos:
, com a 
R,m,n, 
N, a >0, n>0, m>0
Podemos também transformar um radical com expoente fracionário:
Propriedade das potências com expoentes racionais
As propriedades das potências com expoentes racionais são as mesmas para os expoentes inteiros.
Sendo a e b números reais e positivos e os expoentes números racionais, temos que:
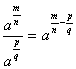
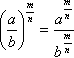
Exemplo:
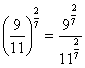
Nenhum comentário:
Postar um comentário