ÂNGULOS CONGRUENTES
Observe os ângulos abaixo:
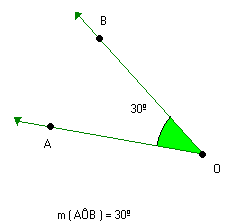
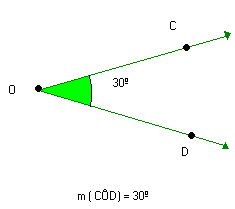
Verifique que AÔB e CÔD têm a mesma medida. Eles são ângulos congruentes e podemos fazer a seguinte indicação:
Assim:
| Dois ângulos são congruentes quando têm a mesma medida. |
Propriedades da Congruência
|
ÂNGULOS CONSECUTIVOS
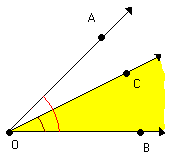
Observe a figura:
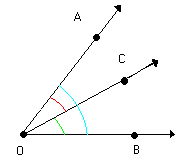
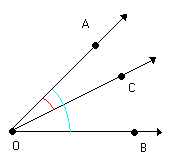
Nela identificamos os ângulos AÔC, CÔB e AÔB.
Verifique em cada uma das figuras abaixo que:
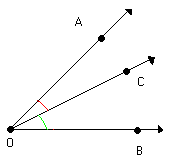 | Os ângulos AÔC e CÔB possuem:Vértice comum: O Lado comum: |
 | Os ângulos AÔC e AÔB possuem:Vértice comum: O Lado comum: |
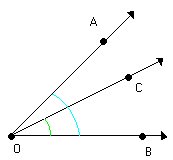 | Os ângulos CÔB e AÔB possuem:Vértice comum: O Lado comum: |
Os pares de ângulos AÔC e CÔB, AÔC e AÔB, CÔB e AÔB são denominados ângulos consecutivos.
Assim:
Dois ângulos são consecutivos quando possuem o mesmo vértice e um lado comum.
ÂNGULOS ADJACENTES
Observe os exemplos de ângulos consecutivos vistos anteriormente e verifique que:
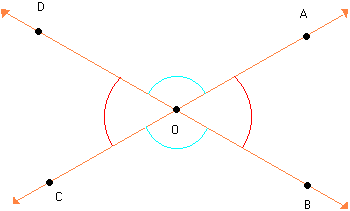
Verifique que os ângulos AÔC e CÔB são consecutivos e não possuem pontos internos comuns. Por isso eles são denominados ângulos adjacentes.
Assim:
Observação:
Duas retas concorrentes determinam vários ângulos adjacentes. Exemplos:
 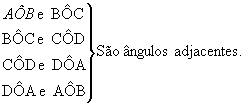
BISSETRIZ DE UM ÂNGULO
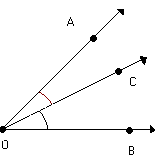
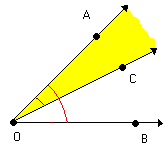
Observe a figura abaixo:
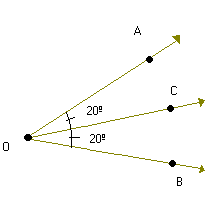 m ( AÔC ) = m (CÔB ) = 20º m ( AÔC ) = m (CÔB ) = 20º
Verifique que a semi-reta
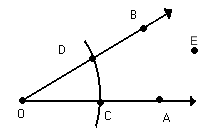
Nesse caso, a semi-reta
Assim:
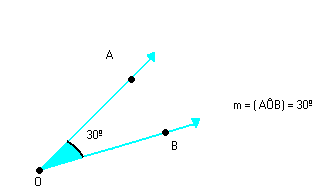
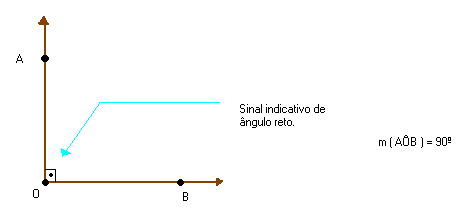
ÂNGULO AGUDO, OBTUSO E RETO
Podemos classificar um ângulo em agudo, obtuso ou reto.
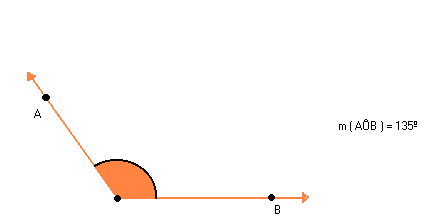
RETAS PERPENDICULARES
As retas r e s da figura abaixo são concorrentes e formam entre si quatro ângulos retos.
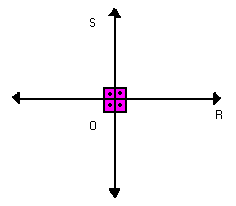
Dizemos que as retas r e s são perpendiculares e indicamos:
Observação
Duas retas concorrentes que não formam ângulos retos entre si são chamadas de oblíquos. Exemplo:
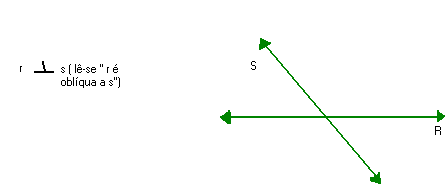 | ||||||||||||||||
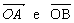 , respectivamente.
, respectivamente.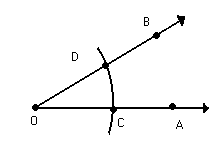
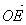 , determinando assim a bissetriz de AÔB.
, determinando assim a bissetriz de AÔB.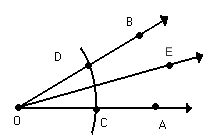
Eu gostei :)
ResponderExcluirsorte sua que eu to no 1 ano do ensino fundamental e já sabia disso a um zilhão de quintilhões de anos atrás.
ExcluirEste comentário foi removido pelo autor.
ResponderExcluirEste comentário foi removido pelo autor.
ResponderExcluirme ajudou bastante mais estou com duvida ainda
ResponderExcluir